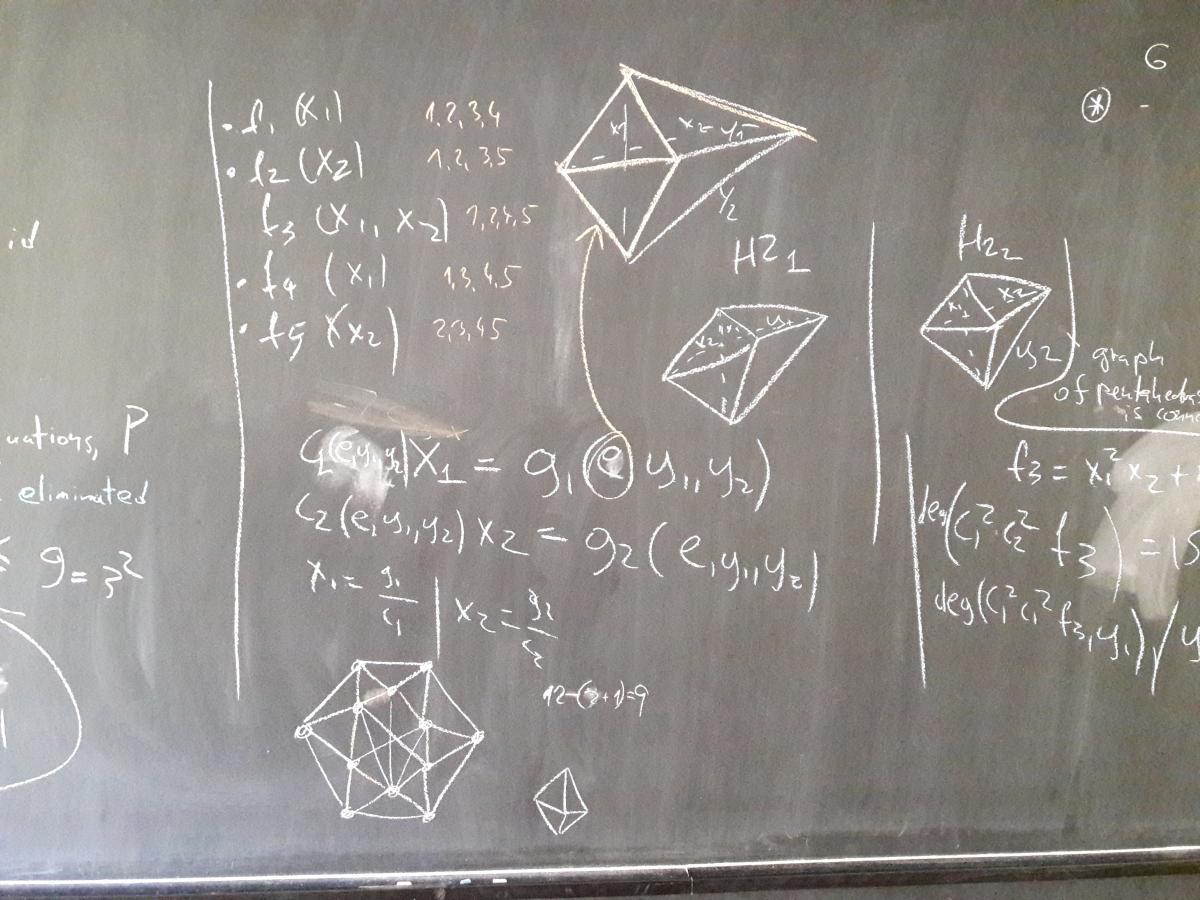Members

Bruno Buchberger: Founding Chairman 1987-1998

Eriola Hoxhaj

Günter Landsmann

Josef Schicho

Franz Winkler: Chairman 1999-2009

Software
desing homepage ...
CASA is a special-purpose system for computational algebra and constructive algebraic geometry. The system has been developed since 1990, and is the ongoing product of the Computer Algebra Group under the direction of Prof. Winkler. It is built on the ...
CharSet is an Aldor package written by Christian Aistleitner for differential characteristic set computations. CharSet comes with generic implementations of reduction, Gröbner bases, and differential characteristic set algorithms. Interfaces to the command line, Mathematica and Maple are included. ...
PGB is a software package for computing parametric Gröbner bases and related objects in several domains. It is implemented in the computer algebra system Risa/Asir by Katsusuke Nabeshima. ...
Publications
2023
Automated Programming, Symbolic computation, Machine Learning: My Personal View
Bruno Buchberger
Ann. Math. Artif. Intell. 91(5), pp. 569-589. 2023. 1012-2443.author = {Bruno Buchberger},
title = {{Automated Programming, Symbolic computation, Machine Learning: My Personal View}},
language = {english},
journal = {Ann. Math. Artif. Intell.},
volume = {91},
number = {5},
pages = {569--589},
isbn_issn = {1012-2443},
year = {2023},
refereed = {yes},
length = {21}
}
International Young Talents Hotspot Austria
Bruno Buchberger
In: Ideen, die gehen!, W. Schüssel, G. Kneifel (ed.), pp. 37-39. 2023. Edition Kleine Zeitung, 20234.author = {Bruno Buchberger},
title = {{International Young Talents Hotspot Austria}},
booktitle = {{Ideen, die gehen!}},
language = {english},
pages = {37--39},
publisher = {Edition Kleine Zeitung},
isbn_issn = {20234},
year = {2023},
editor = {W. Schüssel and G. Kneifel},
refereed = {no},
length = {3}
}
Wissenschaft und Meditation: Auf dem Weg zur bewussten Naturgesellschaft
Bruno Buchberger
1st edition, December 2023. Amazon, 979-8868299117.author = {Bruno Buchberger},
title = {{Wissenschaft und Meditation: Auf dem Weg zur bewussten Naturgesellschaft}},
language = {german},
publisher = {Amazon},
isbn_issn = {979-8868299117},
year = {2023},
month = {December},
edition = {1st},
translation = {0},
length = {184}
}
Using Algebraic Geometry to Reconstruct a Darboux Cyclide from a Calibrated Camera Picture
E. Hoxhaj, J.-M. Menjanahary, J. Schicho
J. AAECC, pp. -. 2023. 1432-0622. to appear. [doi]author = {E. Hoxhaj and J.-M. Menjanahary and J. Schicho},
title = {{Using Algebraic Geometry to Reconstruct a Darboux Cyclide from a Calibrated Camera Picture}},
language = {english},
journal = {J. AAECC},
pages = {--},
isbn_issn = {1432-0622},
year = {2023},
note = {to appear},
refereed = {yes},
length = {19},
url = {https://doi.org/10.1007/s00200-023-00600-y}
}
Representing piecewise linear functions by functions with small arity
C. Koutschan, B. Moser, A. Ponomarchuk, J. Schicho
J. AAECC, pp. -. 2023. 1432-0622.author = {C. Koutschan and B. Moser and A. Ponomarchuk and J. Schicho},
title = {{Representing piecewise linear functions by functions with small arity}},
language = {english},
journal = {J. AAECC},
pages = {--},
isbn_issn = {1432-0622},
year = {2023},
refereed = {yes},
length = {0}
}
General solutions of first-order algebraic ODEs in simple constant extensions
J. J. Mitteramskogler, F. Winkler
Journal of Systems Science and Complexity (JSSC), pp. 0-0. 2023. 1009-6124.author = {J. J. Mitteramskogler and F. Winkler},
title = {{General solutions of first-order algebraic ODEs in simple constant extensions}},
language = {english},
journal = {Journal of Systems Science and Complexity (JSSC)},
pages = {0--0},
isbn_issn = {1009-6124},
year = {2023},
refereed = {yes},
length = {0}
}
Trilinear birational maps in dimension three
L. Buse, P. Gonz'alez-Maz'on, J. Schicho
M. Comp. 92, pp. 1837-1866. 2023. 0025-5718.author = {L. Buse and P. Gonz'alez-Maz'on and J. Schicho},
title = {{Trilinear birational maps in dimension three}},
language = {english},
journal = {M. Comp.},
volume = {92},
pages = {1837--1866},
isbn_issn = {0025-5718},
year = {2023},
refereed = {yes},
length = {30}
}
Apollonian-de Casteljau type algorithms for complex rational Bezier curves
B. J�ttler, J. Schicho, Z. Sir
CAGD 107, pp. -. 2023. 0167-8396.author = {B. J�ttler and J. Schicho and Z. Sir},
title = {{Apollonian-de Casteljau type algorithms for complex rational Bezier curves}},
language = {english},
journal = {CAGD},
volume = {107},
pages = {--},
isbn_issn = {0167-8396},
year = {2023},
refereed = {yes},
length = {0}
}
2022
On Formal Power Series Solutions of Algebraic Ordinary Differential Equations
S. Falkensteiner, Yi Zhang, N. Thieu Vo
Mediterranean Journal of Mathematics 19(74), pp. 1-16. March 2022. ISSN 1660-5446. [doi]author = {S. Falkensteiner and Yi Zhang and N. Thieu Vo},
title = {{On Formal Power Series Solutions of Algebraic Ordinary Differential Equations}},
language = {english},
journal = {Mediterranean Journal of Mathematics},
volume = {19},
number = {74},
pages = {1--16},
isbn_issn = {ISSN 1660-5446},
year = {2022},
month = {March},
refereed = {yes},
keywords = {Formal power series, algebraic differential equation.},
length = {16},
url = {https://doi.org/10.1007/s00009-022-01984-w}
}
Zero-Sum Cycles in Flexible Non-triangular Polyhedra
Matteo Gallet, Georg Grasegger, Jan Legerský, Josef Schicho
In: 2nd IMA Conference on Mathematics of Robotics, W. Holderbaum, J.M. Selig (ed.), Springer Proceedings in Advanced Robotics 21, pp. 137-143. 2022. 978-3-030-91351-9. [doi]author = {Matteo Gallet and Georg Grasegger and Jan Legerský and Josef Schicho},
title = {{Zero-Sum Cycles in Flexible Non-triangular Polyhedra}},
booktitle = {{2nd IMA Conference on Mathematics of Robotics}},
language = {english},
series = {Springer Proceedings in Advanced Robotics},
volume = {21},
pages = {137--143},
isbn_issn = {978-3-030-91351-9},
year = {2022},
editor = {W. Holderbaum and J.M. Selig},
refereed = {yes},
length = {7},
url = {https://doi.org/10.1007/978-3-030-91352-6_14}
}
Zero-sum Cycles in Flexible Polyhedra
M. Gallet, G. Grasegger, J. Legersky, J. Schicho
Bull. LMS 54, pp. 112-125. 2022. 1469-2120.author = {M. Gallet and G. Grasegger and J. Legersky and J. Schicho},
title = {{Zero-sum Cycles in Flexible Polyhedra}},
language = {english},
journal = {Bull. LMS},
volume = {54},
pages = {112--125},
isbn_issn = {1469-2120},
year = {2022},
refereed = {yes},
length = {14}
}
Approximation of convex polygons by polygons
C. Koutschan, A. Ponomarchuk, J. Schicho
In: 23rd International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), C. Schneider et al. (ed.), pp. 91-98. 2022. IEEE, 978-1-6654-0650-5.author = {C. Koutschan and A. Ponomarchuk and J. Schicho },
title = {{Approximation of convex polygons by polygons}},
booktitle = {{23rd International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC)}},
language = {english},
pages = {91--98},
publisher = {IEEE},
isbn_issn = {978-1-6654-0650-5},
year = {2022},
editor = {C. Schneider et al.},
refereed = {yes},
length = {8}
}
Symbolic solutions of algebraic ODEs - A comparison of methods
J. J. Mitteramskogler, F. Winkler
Publicationes Mathematicae Debrecen 100(1-2), pp. 143-166. 2022. 0033-3883.author = {J. J. Mitteramskogler and F. Winkler},
title = {{Symbolic solutions of algebraic ODEs -- A comparison of methods}},
language = {english},
journal = {Publicationes Mathematicae Debrecen},
volume = {100},
number = {1-2},
pages = {143--166},
isbn_issn = {0033-3883},
year = {2022},
refereed = {yes},
length = {23}
}
And Yet it Moves - Paradoxically Moving Linkages in Kinematics
J. Schicho
Bulletin AMS 59, pp. 59-95. 2022. ISSN 0273-0979. [doi]author = {J. Schicho},
title = {{And Yet it Moves -- Paradoxically Moving Linkages in Kinematics}},
language = {english},
journal = {Bulletin AMS},
volume = {59},
pages = {59--95},
isbn_issn = {ISSN 0273-0979},
year = {2022},
refereed = {yes},
length = {37},
url = {https://doi.org/10.1090/bull/1721}
}
Classification of higher mobility closed-loop linkages
T. Duarte Guerreiro, Z. Li, J. Schicho
Annali di Matematica Pura et Applicata, pp. -. 2022. 0373-3114.author = {T. Duarte Guerreiro and Z. Li and J. Schicho},
title = {{Classification of higher mobility closed-loop linkages}},
language = {english},
journal = {Annali di Matematica Pura et Applicata},
pages = {--},
isbn_issn = {0373-3114},
year = {2022},
refereed = {yes},
length = {0}
}
A new line-symmetric mobile infinity-pod
M. Gallet, J. Schicho
Confl. Math. 14, pp. 35-47. 2022. 1793-7442.author = {M. Gallet and J. Schicho},
title = {{A new line-symmetric mobile infinity-pod}},
language = {english},
journal = {Confl. Math.},
volume = {14},
pages = {35--47},
isbn_issn = {1793-7442},
year = {2022},
refereed = {yes},
length = {13}
}
Projective isomorphisms between rational surfaces
B. J�ttler, N. Lubbes, J. Schicho
J. Algebra 54, pp. 112-125. 2022. 0021-8693.author = {B. J�ttler and N. Lubbes and J. Schicho},
title = {{Projective isomorphisms between rational surfaces}},
language = {english},
journal = {J. Algebra},
volume = {54},
pages = {112--125},
isbn_issn = { 0021-8693},
year = {2022},
refereed = {yes},
length = {14}
}
2021
Combinatorics of Bricard's octahedra
M. Gallet, G. Grasegger, J. Legerský, J. Schicho
Comptes Rendus. Mathématique 359(1), pp. 7-38. 2021. Académie des sciences, Paris, ISSN 1631-073X. [doi]author = {M. Gallet and G. Grasegger and J. Legerský and J. Schicho},
title = {{Combinatorics of Bricard's octahedra}},
language = {english},
journal = {Comptes Rendus. Mathématique},
volume = {359},
number = {1},
pages = {7--38},
publisher = {Académie des sciences, Paris},
isbn_issn = {ISSN 1631-073X},
year = {2021},
refereed = {yes},
length = {32},
url = {https://doi.org/10.5802/crmath.132}
}
On the Existence of Paradoxical Motions of Generically Rigid Graphs on the Sphere
M. Gallet, G. Grasegger, J. Legerský, J. Schicho
SIAM Journal on Discrete Mathematics 35(1), pp. 325-361. 2021. ISSN 0895-4801. [doi]author = {M. Gallet and G. Grasegger and J. Legerský and J. Schicho},
title = {{On the Existence of Paradoxical Motions of Generically Rigid Graphs on the Sphere}},
language = {english},
journal = {SIAM Journal on Discrete Mathematics},
volume = {35},
number = {1},
pages = {325--361},
isbn_issn = {ISSN 0895-4801},
year = {2021},
refereed = {yes},
length = {37},
url = {https://doi.org/10.1137/19M1289467}
}
On the maximal number of real embeddings of minimally rigid graphs in R2, R3 and S2
E. Bartzos, I.Z. Emiris, J. Legerský, E. Tsigaridas
Journal of Symbolic Computation 102, pp. 189-208. 2021. ISSN 0747-7171. [doi]author = {E. Bartzos and I.Z. Emiris and J. Legerský and E. Tsigaridas},
title = {{On the maximal number of real embeddings of minimally rigid graphs in R2, R3 and S2}},
language = {english},
journal = {Journal of Symbolic Computation},
volume = {102},
pages = {189--208},
isbn_issn = {ISSN 0747-7171},
year = {2021},
refereed = {yes},
length = {20},
url = {https://doi.org/10.1016/j.jsc.2019.10.015}
}