Studying Symbolic Computation
Symbolic computation is the sub-area of mathematics and computer science which solves problems on symbolic objects representable on a computer. Typical examples of such objects are
- algebraic expressions,
- logical propositions, and
- programs themselves.
The problem solutions are integrated in many advanced software systems for computer algebra, computer aided design and manufacturing, computer supported reasoning, knowledge management, and formal system specification and verification. Besides playing a fundamental role within mathematics itself, symbolic computation is thus a key technology in many scientific and technical areas today.
More than any other area, symbolic computation depends on the integration of the
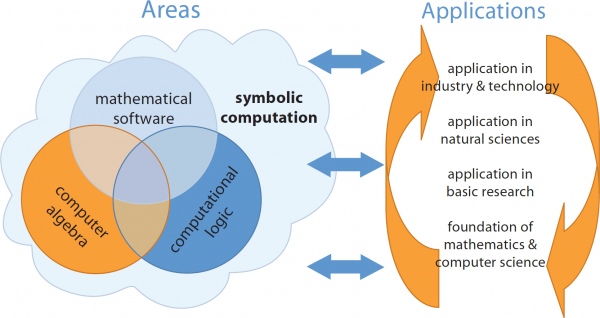
- theoretical foundations (mathematics, logics, algorithms),
- the implementation in software systems, and the
- practical applications.
It is a main objective of the symbolic computation curriculum at RISC to unite these three aspects. Graduates of this program are not only experts in symbolic computation but, due to their work in highly abstract models with the goal to develop effective software solutions, also professionals in developing innovative computer-based solutions for challenging problems arising in theoretical investigations and real-world applications. Therefore they are highly qualified to find their place in research and development, in academia and industry.
Within the realm of symbolic computation, research at RISC mainly falls into three general categories:
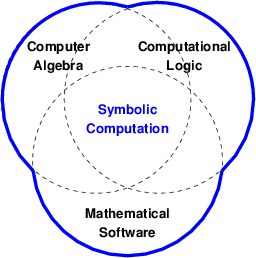 Computer Algebra
Computer Algebra- We design and implement algorithms that operate on algebraic expressions; typical application areas are e.g. (algebraic) geometry and (algorithmic) combinatorics.
- Computational Logic
- We work on the specification, management, and derivation of knowledge expressed in the language of symbolic logic (resulting in software systems for supporting mathematical proving) and on the theory of computation.
- Mathematical Software
- We develop various symbolic computation software such as it occurs in computer algebra systems and theorem provers and study the logical foundations of software for the purpose of formal system specification and verification.
These categories (which present different views to the same field with strong overlappings and interrelationships) are also reflected in the RISC curriculum. See this list of applications for sample outcomes of this research.
RISC Courses
RISC offers three kinds of courses:
- Curriculum Courses
- These are the core courses of the curriculum; every Ph.D. student performs course work in the amount of at least 30 ECTS points. The curriculum courses are offered annually or biennially; additionally Special Topics courses with varying content may be offered.
- Seminars
- In seminars, the RISC faculty discusses the state of the art in research and ongoing project work. In the first year, every Ph.D. student attends (as a listener) several seminars; later the student attends (as an active participant) at least one seminar per semester. Seminar topics vary from semester to semester, the ones listed below are just examples.
- Standard Courses
- These are courses offered by RISC for bachelor/master students in mathematics or computer science. They are actually not part of the RISC curriculum but they may help in exceptional cases to supplement the education of new Ph.D. students.
According to the general working areas of RISC, the courses are structured into three categories. Short course descriptions are given in the appendix.
Computer Algebra
Curriculum Courses
| Title | ECTS | Period |
|---|---|---|
| Computer Algebra | 4.5 | annually |
| Gröbner Bases | 3 | biennially |
| Fast Arithmetic and Factorization | 3 | biennially |
| Elimination Theory | 3 | biennially |
| Commutative Algebra and Algebraic Geometry | 7.5 | biennially |
| Algorithmic Algebraic Geometry | 3 | biennially |
| Computer Analysis | 3 | biennially |
| Symbolic Linear Algebra | 3 | biennially |
| Computer Algebra for Concrete Mathematics | 4.5 | annually |
| Algorithmic Combinatorics | 4.5 | annually |
| Symbolic Summation and Special Functions 1 | 3 | biennially |
| Symbolic Summation and Special Functions 2 | 3 | biennially |
| Category Theory for Symbolic Computation | 3 | biennially |
| Algebraic Methods in Kinematics | 3 | biennially |
| Algebraic Topology | 3 | biennially |
| Homological Algebra | 3 | biennially |
| Special Topics in Computer Algebra | 3 | on demand |
Seminars (Examples)
- Seminar “Computer Algebra”
- Seminar “Algorithmic Algebra”
- Seminar “Algorithmic Combinatorics
- Seminar “Algebraic Geometry”
- Seminar “Symbolic Summation for Particle Physics”
- Seminar “Symbolic Summation and Special Functions”
- Seminar “Fundamentals of Numerical Analysis and Symbolic Computation”
Standard Courses
- Algebra
- Analysis
- Linear Algebra 1 and 2
- Linear Algebra for Physicists 1 and 2
- Linear Algebra and Analytic Combinatorics 1 and 2
- Linear Algebra and Analytic Geometry 1 and 2
- Ordinary Differential Equations and Dynamical Systems 1
- Algebraic and Discrete Methods for Biology
- Preparatory Course Mathematics for Beginners of Business Informatics
Computational Logic
Curriculum Courses
| Title | ECTS | Period |
|---|---|---|
| Thinking, Speaking, Writing 1+2 | 6 | annually |
| Mathematical Logic | 7.5 | annually |
| Topics in Mathematical Logic | 3 | biennially |
| Automated Reasoning | 3 | biennially |
| Advanced Automated Reasoning | 3 | biennially |
| Computability Theory | 3 | biennially |
| Decidability and Complexity Classes | 3 | biennially |
| Decidable Logical Theories | 3 | biennially |
| Rewriting in Computer Science and Logic | 3 | biennially |
| Unification Theory | 3 | biennially |
| Gödel’s Incompleteness Theorems | 3 | biennially |
| Formal Methods in Software Development | 4.5 | annually |
| Formal Semantics of Programming Languages | 3 | biennially |
| Formal Specification of Abstract Datatypes | 3 | biennially |
| Formal Models of Parallel a. Distributed Systems | 3 | biennially |
| Formal Languages and Formal Grammars 1 | 3 | biennially |
| Formal Languages and Formal Grammars 2 | 3 | biennially |
| Fixpoint Theory of Functional Programs | 3 | biennially |
| Special Topics in Computational Logic | 3 | on demand |
Seminars (Examples)
- Seminar “Automated Reasoning (Theorema)”
- Seminar “Set Theory and Logical Foundations”
- Seminar “Formal Methods”
Standard Courses
- Logic as a Working Language
- Logic for Computer Science
- Mathematics and Logic
- Computability and Complexity
- Formal Foundations in Business Informatics
Mathematical Software
Curriculum Courses
| Title | ECTS | Period |
|---|---|---|
| Programming Project Symbolic Computation 1+2 | 6 | annually |
| Design and Analysis of Algorithms | 3 | biennially |
| Introduction to Parallel and Distributed Computing | 3 | biennially |
| Logic Programming | 3 | annually |
| Functional Programming | 3 | annually |
| Programming in Mathematica | 3 | annually |
| Chess Programming | 3 | biennially |
| Computer Algebra Systems | 3 | biennially |
| Automated Reasoning Systems | 3 | biennially |
| Computer-based Working Environments | 1.5 | annually |
| Special Topics in Mathematical Software | 3 | on demand |
Seminars (Examples)
- Bachelor Seminar “Selected Algorithms in Symbolic Computation”
Standard Courses
- Practical Software Technology
- Software Engineering
- Project Engineering
- Algorithms and Data Structures
- Information Systems
- Computer Systems
- Algorithmic Methods 1
Course Descriptions
In the following, we give short descriptions of the courses of the RISC curriculum.
Computer Algebra
- Computer Algebra: ECTS 4.5, annually.
- A theoretical introduction to the area of computer algebra is presented. The list of topics includes basic algebraic domains, greatest common divisors of polynomials, the Chinese remainder algorithm, factorization of polynomials, and the theory of Gröbner bases.
- Gröbner Bases: ECTS 3, biennially.
- The algorithmic theory of Gröbner bases is one of the outstanding tools in mathematics that enables one to tackle “in principal a huge class of problems arising in sciences, in particular in mathematics and computer sciences. In this lecture the underlying concepts are worked out and Buchberger’s distinguished algorithm and their optimized variants are discussed. Special emphasis is put on applications, in particular, on how non-trivial problems of sciences can be formulated into the setting of Gröbner basis theory and on how they can be attacked with the available algorithms.
- Fast Arithmetic and Factorization: ECTS 3, biennially.
- How many field operations are needed to multiply two univariate polynomials of degree n over some field K? How about the number of field operations needed for factoring a polynomial or computing a greatest common divisor of two polynomials? Efficient algorithms for these and other problems were presented in Computer Algebra I, but are they as efficient as can be? It turns out that they are not. In Computer Algebra II we will present faster algorithms, including some of the fastest algorithms known today for solving algebraic problems
- Elimination Theory: ECTS 3, biennially.
- This course is concerned with algorithmic approaches to the solution of polynomial equations. Typical approaches include resultants, Gröbner bases and characteristic sets.
- Commutative Algebra and Algebraic Geometry: ECTS 7.5, biennially.
- In this course the relation between the algebraic theory of polynomial ideals and the geometry of curves, surfaces, and algebraic varieties is described. Topics include Hilbert’s basis theorem, Hilbert’s Nullstellensatz, polynomial and rational functions on varieties, singular points, parametrizations, and determination of dimension.
- Algorithmic Algebraic Geometry: ECTS 3, biennially.
- Algebraic Geometry aims at the understanding of the structure of algebraic varieties, which are defined as the solution sets of algebraic equation systems. As this branch of mathematics has a long and rich history, the amount of available theorems is enormous. In Algorithmic AG, we have a look at some of these results from the constructive point of view: instead of being content with the mere existence of some structure (like singularity resolution, special divisors, fibrations), we want to compute it effectively.
- Computer Analysis: ECTS 3, biennially.
- Symbolic methods for integration and the analysis and solution of differential equations are described.
- Symbolic Linear Algebra: ECTS 3, biennially.
- In many applications of symbolic computation (e.g., summation, integration, solving difference/differential equations) one has to solve systems of linear equations that are not defined over floating-point numbers, but for instance over rational function fields or over principle ideal domains. In this lecture we discuss how to generalize and/or optimize the well-known linear algebra methods in order to solve such systems. The application of these methods are illustrated by various examples.
- Computer Algebra for Concrete Mathematics: ECTS 4.5, annually.
- The major topics of this course include sums, recurrences, elementary number theory, binomial coefficients, generating functions, and asymptotic methods. The emphasis is on manipulative technique rather than on existence theorems or combinatorial reasoning. Theoretical exposition will be supplemented by computer algebra methods like Zeilberger’s algorithm. (Literature: “Concrete Mathematics – A Foundation for Computer Science by R.L. Graham, D.E. Knuth und O. Patashnik, and other books and papers.)
- Algorithmic Combinatorics: ECTS 4.5, annually.
- The course provides an introduction to enumerative combinatorics. Topics are: special sequences like Stirling numbers, partition theory, and important general concepts like group actions and Polya’s counting theory. Theoretical exposition will be supplemented by computer algebra methods.
- Symbolic Summation and Special Functions 1: ECTS 3, biennially.
- Some functions from analysis arise so often in applications that we give them special names. Paul Turan once remarked that such special functions would be more appropriately labeled “useful functions. Beginning with Newton and Leibniz, special functions have been continuously developed, including significant contributions by Euler, Legendre, Laplace, Gauss, Kummer, Eisenstein, and Riemann. In recent years the interest in special functions has been renewed, also due to new computer algebra applications. The lecture introduces to fundamental themes like gamma function, hypergeometric series, and Bessel functions. Theoretical exposition will be supplemented by computer algebra methods. (Literature: “Special Functions by G.E. Andrews, R. Askey, and R. Roy.) The lecture introduces also the theoretical foundations of symbolic summation: greatest factorial factorization (GFF) in connection with indefinite summation of rational and hypergeometric sequences. As applications, famous algorithms as those of Gosper and Zeilberger are discussed.
- Symbolic Summation and Special Functions 2: ECTS 3, biennially.
- The course is designed in such a way that it can be followed independently from having attended “Special Functions 1. Topics include: orthogonal polynomials (e.g., Chebyshev, Hermite, Laguerre, Jacobi) and related themes like the irrationality of the Riemann zeta function at z=3; in addition, an introduction to q-series is provided. As in Part I, theoretical exposition will be supplemented by computer algebra methods. (Literature: “Special Functions by G.E. Andrews, R. Askey, and R. Roy.) Based on works by Karr, the lecture also presents a difference field approach to symbolic summation. It can be seen as a discrete analogon to Risch integration theory. Due to work of Schneider, various extensions of Karr’s theory have become a powerful tool which can be used in highly nontrivial applications in special functions, combinatorics, physics, etc.
- Category Theory for Symbolic Computation: ECTS 3, biennially.
- Directional structures between two objects occur widely in mathematics and computer science. Category theory emerged as a frame for formalizing such arrow concepts. Its capacious applicability originates from describing structure in terms of the existence of arrows and relations between them rather than intrinsic properties of objects. Categories themselves arise as abstraction of essentially algebraic theories. Besides its non-constructive parts category theory is concerned with concepts which are mainly algorithmic in nature. In this course we concentrate on this particular aspect of the theory.
- Algebraic Methods in Kinematics: ECTS 3, biennially.
- In kinematics, the motions of rigid bodies are described by concepts like position, orientation, velocity etc. These concepts are related to the group of Euclidean displacements. This group and the class of functions into it describing motions can be described efficiently and investigated by means of quaternions, Lie groups, or algebraic geometry. These descriptions will be explained and applied to typical problems in kinematics, such as the construction of linkages generating a prescribed motion, or the classification of overconstrained linkages.
- Algebraic Topology: ECTS 3, biennially.
- The course gives an introduction to algebraic topology. After developing the central concepts of homotopy theory we discuss several homology theories. Then the relations between these approaches are considered. The necessary categorical language will be explained on demand.
- Homological Algebra: ECTS 3, biennially.
- Since their emergence in algebraic topology, homological concepts have proved their efficiency in several mathematical disciplines. Homological algebra is the theory of these concepts formulated in an abstract categorical setting. After introducing the basic categories of chain complexes and their homotopy categories we proceed towards derived functors on abelian categories. The final lectures are devoted to the development of spectral sequences.
- Special Topics in Computer Algebra: ECTS 3, on demand.
Computational Logic
- Thinking, Speaking, Writing 1+2: ECTS 6, annually.
- TSW 1: Understanding and creating mathematical proofs. RISC is one of the few institutes in the world offering the lecture “Thinking, Speaking, Writing, whose purpose is to train the student in all activities involved in scientific work. The first part of the course consists in training in formal reasoning: understanding formal mathematical texts, formalizing mathematical notions, and especially working with formal mathematical texts (proving). As we consider the ability to develop correct proofs as being at the very core of the activity in computer mathematics, the lecture consists in intensive training in basic proof techniques and in-depth understanding and mastering of formal mathematics.
- TSW 2: Communication of scientific results.
- The career of a scientist relies heavily of his ability to communicate his results through scientific publications and conference talks. The second part of TSW teaches the basic principles and trains the abilities necessary to communication of scientific results in an effective and efficient manner. The subjects include: presentation of scientific results in oral and written form, working with the scientific literature, attending scientific presentations, and cooperating in research groups.
- Mathematical Logic: ECTS 7.5, annually.
- The course is an introduction to logic for students in Computer Science and Mathematics. The purpose of the course is to understand the principles of Mathematical Logic and its mathematical models, and to acquire the skills for using it in Mathematics and Computer Science. The course covers the main models: propositional logic, first-order predicate logic, higher-order logic, as well as the main proof systems for these models. Furthermore the lecture demonstrates and trains the practical use of Mathematical Logic in Mathematics (building theories, proving), and in Computer Science (automatic reasoning, programming, describing and proving properties of programs).
- Topics in Mathematical Logic: ECTS 3, biannually.
- In this course some deeper results in the area of predicate logic are presented, like Gödel’s completeness theorem, omitting types theorem, Craig’s interpolation theorem, Gödel’s incompleteness theorem, as well as applications of elementary chains and ultraproducts.
- Automated Reasoning: ECTS 3, biennially.
- Introduction to Automated Reasoning: This course presents and compares the basic methods for Automated Reasoning: the resolution method and the main methods for proving in natural style. The topics of the lecture are: syntax and semantics of logical formulae, normalization of formulae, the Herbrand Theorem, the proof method by resolution, the sequent calculus and its use in automated reasoning, basic methods for reasoning with equality. Some concrete implementations will be also presented, including the implementation in Theorema of natural style proving, as well as some applications of automated reasoning in Mathematics and Computer Science.
- Advanced Automated Reasoning: ECTS 3, biennially.
- Advanced Topics in Automated Reasoning: This course presents and compares some advanced methods for automated reasoning: refinements of the resolution method, the use of paramodulation for theories with equality, search strategies in natural style proving, the use of meta-variables in sequent calculus, natural deduction for theories with equality and the Knuth-Bendix completion method, methods for combining general and domain specific reasoning, logic-based algorithm synthesis. The course will also present some practical implementations of these methods, including natural deduction in the Theorema system, as well as current applications of automated reasoning in Mathematics and Computer Science.
- Computability Theory: ECTS 3, biennially.
- This course deals not with algorithms for specific problems, but with the notion of computability itself. This means that the class of algorithmically computable (partial recursive) functions is investigated mathematically. Among other things it is shown that certain problems are algorithmically undecidable, that is, they cannot be solved by computer programs even in principle.
- Decidability and Complexity Classes: ECTS 3, biennially.
- The first part of this course is a sequel to Computability Theory. Algorithmically undecidable problems may be reduced to each other and thus compared with respect to the degree of undecidability. The second part deals with various aspects of abstract complexity theory, including NP-completeness.
- Decidable Logical Theories: ECTS 3, biennially.
- In this course decision algorithms are given for various logical theories, specifically, for the set of all true sentences in some model or the set of all consequences of some set of axioms. Some examples are Presburger arithmetic, and the theories of real closed fields, Abelian groups and linear orderings. Various basic methods for developing such decision algorithms are introduced, the most important being quantifier elimination.
- Rewriting in Computer Science and Logic: ECTS 3, biennially.
- Equational theories appear in many areas of mathematics, logic, and computer science. Methods for turning a set of equational axioms into an equivalent set of rewrite rules are discussed. The Knuth-Bendix procedure and the Gröbner basis algorithm are typical examples of such transformations.
- Unification theory: ECTS 3, biennially.
- Unification, or equation solving in abstract algebras, has been studied since the beginning of mathematics. It is concerned with the problem of identifying given terms, either syntactically or modulo a given theory. Unification is at the very heart of computation in a given logic: It is the basic operation in automated reasoning, rewriting, completion, logic programming, and in the related areas. This course presents first-order syntactic and equational unification, and higher-order unification and matching.
- Gödel’s Incompleteness Theorems: ECTS 3, biennially.
- Gödel’s incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems for mathematics. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of mathematics. The two results are widely interpreted as showing that Hilbert’s program to find a complete and consistent set of axioms for all of mathematics is impossible, thus giving a negative answer to Hilbert’s second problem. The first incompleteness theorem states that no consistent system of axioms whose theorems can be listed by an “effective procedure” (essentially, a computer program) is capable of proving all facts about the natural numbers. For any such system, there will always be statements about the natural numbers that are true, but that are unprovable within the system. The second incompleteness theorem shows that if such a system is also capable of proving certain basic facts about the natural numbers, then one particular arithmetic truth the system cannot prove is the consistency of the system itself. This course is intended for students of mathematics or computer science who are interested on the theoretical foundations of computer science. There is no particular prerequisite for the course.
- Formal Methods in Software Development: ECTS 4.5, annually.
- This course gives a survey on the theory and practice of formal methods in the development of sequential and concurrent software, as they are more and more used in industrial practice for ensuring the correctness of critical system components. Introducing the logical foundations of of Hoare Calculus, predicate transformers, and programs as relations on system states, we will investigate various tools for program specification (e.g. the Java Modeling Language JML), extended static checking (e.g. Esc/Java2), model checking (e.g. the model checker SPIN), and program verification by computer-supported proving (e.g. the RISC ProgramExplorer).
- Formal Semantics of Programming Languages: ETCS 3, biennially.
- This course describes various approaches to define the meaning of a programming language in a mathematically precise way and to reason on this basis about the constructs of the language. These approaches are denotational semantics (programs as functions on semantic domains), operational semantics (programs as state transitions), and axiomatic semantics (programs described by pre/post-condition pairs). We investigate their core ideas, their domain of applicability, and their relationship.
- Formal Specification of Abstract Datatypes: ECTS 3, biennially.
- This course describes the axiomatic/algebraic approach of specifying abstract datatypes (respectively “classes in object-oriented terminology) in a mathematically precise way. We will introduce the core theory, investigate various application examples, and demonstrate languages and software systems (e.g. CafeOBJ and CASL) for writing, checking, and even executing such specifications.
- Formal Models of Parallel and Distributed Systems: ECTS 3, biennially.
- Concurrent and reactive computing systems are difficult to grasp, because they generally exhibit in different runs different behaviors, due to the time-dependent interleaving of operations from different processes. For an adequate understanding of such systems, formal models are of crucial importance. This course introduces two fundamental approaches to specify the behavior and to reason about the properties of such systems, one based on temporal logic (as exemplified by the Temporal Logic of Actions TLA) and one based on process calculus/algebra (as exemplified by CCS and the pi-Calculus).
- Formal Languages and Formal Grammars 1: ECTS 3, biennially.
- In this course we introduce and study the basic abstract models of computation, namely finite state machines, push down machines, and formal grammars, and their relationships to formal languages. It is also discussed how the abstract computing devices are used to process languages, and hence to solve problems that are of practical relevance. The notion of a formal grammar arises from the need to formalize the informal notions of grammar and language. Many formal grammars were invented and they can be ordered in a natural hierarchy. There are no special prerequisites in terms of specific courses to attend. Students are expected to be familiar with the basic notions of mathematics and with basic proof techniques, as taught in the mathematics courses of the first year.
- Formal Languages and Formal Grammars 2: ECTS 3, biennially.
- Within the first part of the course, we introduced some of the basic notions, e.g, finite state machines, push down machines, and formal grammars, and their relationships to formal languages. Within this part we will introduce the Turing Machine in various ways and see that all of them turn to be equivalent. While the first part of the course was dedicated to the theoretical apparatus needed for contracting syntactically correct programs, the second part will introduce the semantical meaning of a program. In particular, we will introduce a mapping between program texts and computable functions. There are no special prerequisites in terms of specific courses to attend. Students who have not attended the first part of the course may also attend this part — when necessary, we will have some additional exercises in order to fill gaps. Students are expected to be familiar with the basic notions of mathematics and with basic proof techniques, as taught in the mathematics courses of the first year.
- Fixpoint Theory of Functional Programs: ECTS 3, biennially.
- In this course we study the fixpoint theory of programs, developed by D. Scott, and we consider the semantics of programs defined as least fixpoints of recursive operators. The topics we will cover include: Computable, partial, total and recursive functions; Decidable and semidecidable sets. The halting problem; Compact, continuous, effective and recursive operators; Knaster-Tarski, Myhill-Shepherdson and Kleene theorems; Fixpoint induction, Scott induction rule for proving properties of programs. This course is intended for students of mathematics or computer science who are interested on the theoretical foundations of computer science. There is no particular prerequisite for the course.
- Special Topics in Computational Logic: ECTS 3, on demand.
Mathematical Software
- Programming Project Symbolic Computation 1+2: ECTS 6, annually.
- In this programming project, the overall process of the team-oriented development of non-trivial mathematical software using modern development tools is exercised.
- Design and Analysis of Algorithms: ECTS 3, biennially.
- In this course algorithms are presented for specific problems in various areas of mathematics like sorting, graph theory, pattern matching and arithmetic. It also includes the discussion of general principles of algorithm design like `Divide and Conquer’ or dynamic programming, as well as techniques for analyzing the complexity of algorithms.
- Introduction to Parallel and Distributed Computing: ECTS 3, biennially.
- This course gives an introduction to programming parallel and distributed computer systems. We give an overview on parallel computer architectures, discuss the principles of engineering parallel software, and program simple examples in various programming models, e.g. SPMD (single program, multiple data) programming with automatically parallelizing compilers and message passing programming in the MPI (message programming interface) standard.
- Logic Programming: ECTS 3, annually.
- Logic programming paradigm has its roots in deduction, and combines it with the computation of values. This course gives an introduction to logic programming, mainly through the Prolog programming language.
- Functional Programming: ECTS 3, annually.
- The course is an introduction to functional programming and to the Lisp programming language. The course covers the basic principles of functional programming (recursive definition of data structures and program construction using recursion, tail-recursion and its relation to iterative programs), as well as the main constructs of the Lisp language (constructing and accessing lists, conditional and iterative programming constructs, use of Lisp for symbolic computation).
- Programming in Mathematica: ECTS 3, annually.
- This course illustrates the programming language of the well-known symbolic computation system Mathematica. The course is targeted towards students with a strong mathematical background and the exercises always have a mathematical flavor. We concentrate on features of the language, which make programming in Mathematica different from standard procedural programming as taught in the introductory programming courses for students of Mathematics, thus we emphasize pattern matching, rule-based programming style, functional programming style, and graphics programming
- Chess Programming: ECTS 3, biennially.
- In the theoretical part varous tasks are considered which can be done by a computer: playing chess, analyzing and assessing positions, solving chess problems and creating endgame tablebases. The principles involved are partially valid for other games as well. Algorithms are described in an abstract fashion. In the practical part a simple chess-playing program is developed.
- Computer Algebra Systems: ECTS 3, biennially.
- Computer algebra systems are nowadays routinely used in mathematics, science, and engineering for elaborating and solving problems involving symbolic calculations, such as the exact solution of polynomial equations, of indefinite integrals, of sums and recurrences, and much more. Prominent examples of such software are the commercial systems Maple and Mathematica and the open source systems Axiom, GAP, and Maxima. This course trains the practical use of such systems by a number of application examples.
- Automated Reasoning Systems: ECTS 3, biennially.
- Today there exist a number of tools that support formal reasoning in mathematics and computer science, from simple proof checkers to interactive proof assistants, fully automatic decision procedures, and comprehensive theorem proving systems. Examples of such systems are Isabelle/HOL, Coq, ACL2, PVS, and last but not least the Theorema system developed at RISC. This course trains the practical use of such systems by a number of application examples.
- Computer-based Working Environments: ECTS 1.5, annually.
- The GNU/Linux operating system gets nowadays more attention based on its excellent features in security and privacy. Many free and open-source programs are available under GNU/Linux. This course teaches how to get things done in a GNU/Linux system. The course covers topics such as working with desktop environment and working on the command line, including a short introduction to commonly used programs, remote connections, mailing, version control, HTML, OpenPGP, image processing.
- Special Topics in Mathematical Software: ECTS 3, on demand.

